Question video finding the range of an absolute value function from
Table of Contents
Table of Contents
Have you ever struggled with understanding how to draw absolute value functions? Do you find it difficult to visualize how the graph should look? If so, you’re not alone. Many people find themselves struggling with drawing absolute value functions, but fear not, as this post will guide you through the process.
When it comes to drawing absolute value functions, there are several things that can be considered pain points. These include not knowing where to start, not understanding the shape of the graph, and not knowing how to find the coordinates of important points on the graph.
The key to drawing absolute value functions lies in understanding their shape. Absolute value functions are V-shaped graphs that have a vertex at the origin. To draw an absolute value function, start by drawing a straight line through the origin that slopes upwards. Then, draw a mirror image of this line on the other side of the y-axis. The resulting graph should look like a V.
In summary, to draw absolute value functions, start by drawing a straight line through the origin that slopes upwards, and then draw a mirror image of this line on the other side of the y-axis to create a V-shaped graph. Remember to find the coordinates of important points such as the vertex and x-intercepts.
How to draw absolute value functions: Step-by-Step Guide
When I first learned how to draw absolute value functions, I struggled a lot. I found it difficult to visualize how the graph should look, and I didn’t know where to start. However, with practice, I was able to master the skill. Here is a step-by-step guide that can help you draw absolute value functions:
Step 1: Start by drawing the line y = x.
Step 2: Identify the vertex of the graph. The vertex is the point where the graph changes direction. In this case, the vertex is at the origin (0,0).
Step 3: Draw the graph to the right of the vertex by finding the absolute value of the x-coordinates and plotting the corresponding y-coordinates. For example, if the x-coordinate is 1, plot (1,1).
Step 4: Draw the same graph on the left side of the vertex by reflecting the points over the y-axis. For example, if the point (1,1) is on the right side of the vertex, plot (-1,1) on the left side.
Step 5: Connect the points on both sides of the vertex with a straight line. This should result in a V-shaped graph.
Understanding the Transformations of Absolute Value Functions
When it comes to drawing absolute value functions, it’s important to understand how different transformations can affect the shape of the graph. For example, if the absolute value function is multiplied by a positive constant, the graph becomes steeper. If the absolute value function is multiplied by a negative constant, the graph flips upside down. Similarly, adding or subtracting a constant to the absolute value function causes the whole graph to shift up or down.
Finding the Range of Absolute Value Functions
Another important aspect of drawing absolute value functions is finding their range. The range of an absolute value function is the set of all possible output values. To find the range, start by finding the vertex of the function. The range will either be all real numbers greater than or equal to the y-coordinate of the vertex, or all real numbers less than or equal to the y-coordinate of the vertex.
Applications of Absolute Value Functions
Absolute value functions have many real-world applications. For example, they can be used to model relationships between two variables that have a fixed distance from each other. They can also be used to model things like temperature fluctuations or stock prices.
Frequently Asked Questions
Q: How do I find the vertex of an absolute value function?
A: The vertex of an absolute value function is located at (0,0).
Q: What is the range of an absolute value function?
A: The range of an absolute value function is either all real numbers greater than or equal to the y-coordinate of the vertex, or all real numbers less than or equal to the y-coordinate of the vertex.
Q: How does changing the sign of the constant affect the graph of an absolute value function?
A: Changing the sign of the constant in front of the absolute value function flips the graph upside down.
Q: What are some real-world applications of absolute value functions?
A: Absolute value functions can be used to model relationships between two variables that have a fixed distance from each other. They can also be used to model things like temperature fluctuations or stock prices.
Conclusion
In conclusion, drawing absolute value functions may seem intimidating at first, but with practice and a solid understanding of their shape and transformations, it can be mastered. Remember to always start by drawing the line y = x, and to identify the vertex of the graph. Don’t forget to take into account any transformations that may affect the shape and position of the graph. Happy graphing!
Gallery
Graphing Absolute Value Functions Worksheet - Live Worksheet Online

Photo Credit by: bing.com /
Absolute Value Graph - Kesillook
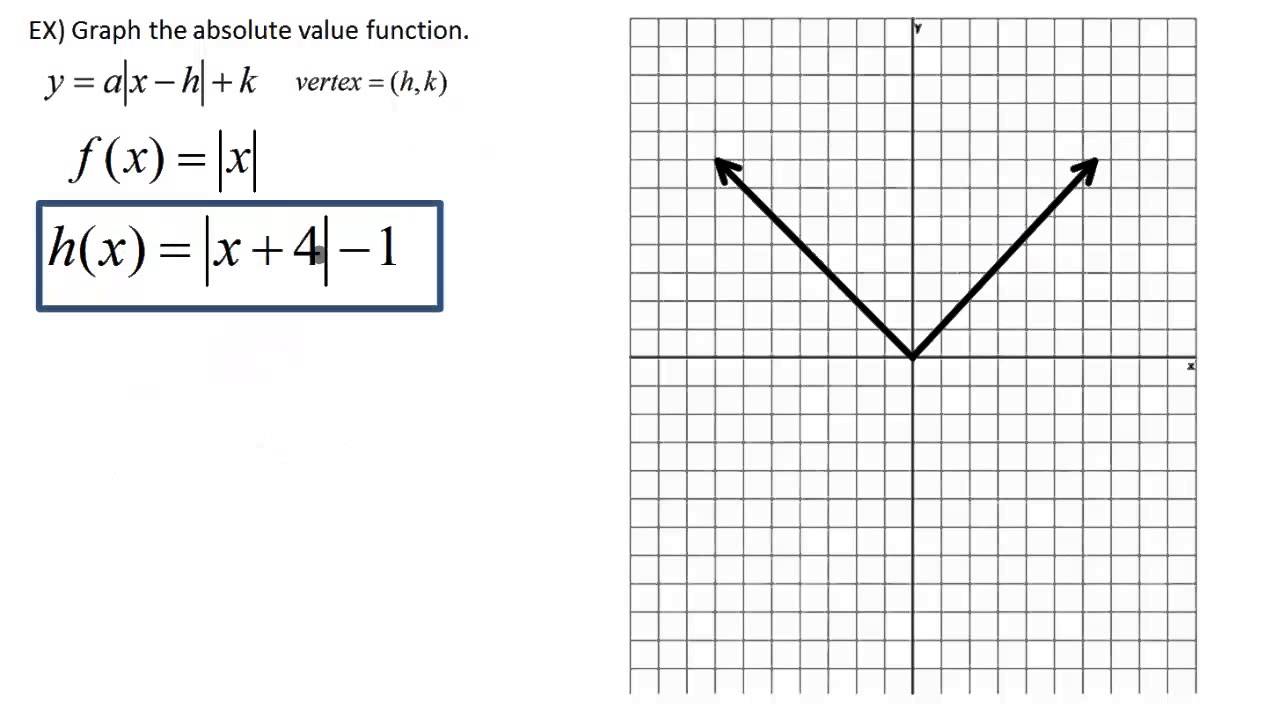
Photo Credit by: bing.com /
3.7 - Graphing Absolute Value Functions - Ms. Zeilstra’s Math Classes

Photo Credit by: bing.com / value absolute graphing functions equations lesson mszeilstra weebly
Draw-absolute-value-number-line - Free Math Worksheets

Photo Credit by: bing.com / value absolute number line draw inequalities graphing math those learn want who definition
Question Video: Finding The Range Of An Absolute Value Function From

Photo Credit by: bing.com / absolute nagwa





