Locus root
Table of Contents
Table of Contents
Are you struggling with drawing root locus by hand in your control systems class? Do you want to improve your skills in this important topic but don’t know where to start? Keep reading to learn more about how to draw root locus by hand and improve your understanding of control systems.
When it comes to control systems, drawing root locus by hand can be a bit challenging. Students often struggle with understanding the concept and making the right calculations. Additionally, some find it difficult to interpret the results of the analysis. This can be frustrating and can also affect their grades.
In order to draw root locus by hand, you need to have a good understanding of the theory behind it. Root locus is a graphical representation of the poles and zeros of a transfer function, as well as the changes in the location of the poles as a parameter is varied. By tracing the locus of the poles, you can analyze the behavior and stability of the system. This is an important tool for control engineers and can be used to design and optimize controllers for a variety of applications.
In summary, to draw root locus by hand, you need to have a good understanding of the theory and practice the calculations. You also need to know how to interpret the results and use them to design and optimize control systems.
My Experience with Drawing Root Locus by Hand
When I first started learning about control systems, I found drawing root locus by hand to be a bit confusing. I struggled with the calculations and understanding how to interpret the results. However, with practice and guidance from my professors, I was able to improve my skills and gain a better understanding of the subject. I found it helpful to use software tools like MatLab to check my work and compare the results.
How to Draw Root Locus by Hand: Step by Step Guide
To draw root locus by hand, follow these steps:
Step 1: Find the transfer function
The first step is to find the transfer function of the system. This can be done by analyzing the system and extracting the relevant equations. The transfer function is the ratio of the output to the input and is typically represented by a fraction of polynomials.
Example
Suppose we have a system with the transfer function:
G(s)= (s+1)(s+2)/(s-1)(s-3)
where s is the Laplace variable.
Step 2: Find the poles and zeros
The next step is to find the poles and zeros of the transfer function. The poles are the values of s that make the denominator of the transfer function equal to zero, while the zeros are the values of s that make the numerator equal to zero.
Example
For the transfer function:
G(s)= (s+1)(s+2)/(s-1)(s-3)
we can find the poles and zeros by setting the numerator and denominator equal to zero:
Numerator:
(s+1)(s+2)=0
s=-1, s=-2
Denominator:
(s-1)(s-3)=0
s=1, s=3
Step 3: Plot the real axis
Plot the real axis on the complex plane. This is the horizontal line through the poles and zeros of the system.
Example
For the transfer function:
G(s)= (s+1)(s+2)/(s-1)(s-3)
we can plot the real axis:
 ### Step 4: Determine the number of branches
### Step 4: Determine the number of branches
Determine the number of branches of the locus, which is equal to the number of poles of the system.
Example
For the transfer function:
G(s)= (s+1)(s+2)/(s-1)(s-3)
we have two poles at s=1 and s=3, so we have two branches.
Step 5: Determine the angles
Determine the angles of departure and arrival for each branch. The angle of departure is the angle between the real axis and the line connecting a pole and a zero. The angle of arrival is the angle between the real axis and the line connecting a pole and a zero.
Example
For the transfer function:
G(s)= (s+1)(s+2)/(s-1)(s-3)
we can find the angles of departure and arrival for each branch:
Branch 1:
Angle of departure at s=-1: θd= 135°
Angle of arrival at s=1: θa= -135°
Branch 2:
Angle of departure at s=-2: θd= 135°
Angle of arrival at s=3: θa= -135°
Step 6: Determine the breakaway and break-in points
Determine the breakaway and break-in points. These are the points where the locus changes direction or crosses the imaginary axis.
Example
For the transfer function:
G(s)= (s+1)(s+2)/(s-1)(s-3)
we can find the breakaway and break-in points:
Breakaway point: s=-0.5+j1.12
Break-in points: s=-0.5-j1.12, s=2.5+j1.12, s=2.5-j1.12
Tips for Drawing Root Locus by Hand
Here are some tips to keep in mind when drawing root locus by hand:
- Make sure to double-check your calculations and plots.
- Use software tools to check your work and compare the results.
- Practice as much as you can to improve your skills.
Question and Answer
Q: What is root locus?
A: Root locus is a graphical representation of the poles and zeros of a transfer function, as well as the changes in the location of the poles as a parameter is varied. By tracing the locus of the poles, you can analyze the behavior and stability of the system.
Q: Why is root locus important in control systems?
A: Root locus is an important tool for control engineers and can be used to design and optimize controllers for a variety of applications. By analyzing the behavior and stability of the system, engineers can make better decisions about how to control it.
Q: Can root locus be drawn by hand?
A: Yes, root locus can be drawn by hand. However, it requires a good understanding of the theory and practice of the calculations.
Q: What are the common mistakes when drawing root locus by hand?
A: Common mistakes when drawing root locus by hand include miscalculations of angles and breakaway/break-in points, incorrect determination of the number of branches, and misinterpretation of the results.
Conclusion of How to Draw Root Locus by Hand
Now that you have a better understanding of how to draw root locus by hand, you can improve your skills and gain confidence in this important topic. Remember to practice as much as you can and use software tools to check your work. Drawing root locus by hand may take some time to master, but with patience and dedication, you can become an expert in no time.
Gallery
3.3 Root Locus Sketching (Part 1) - YouTube
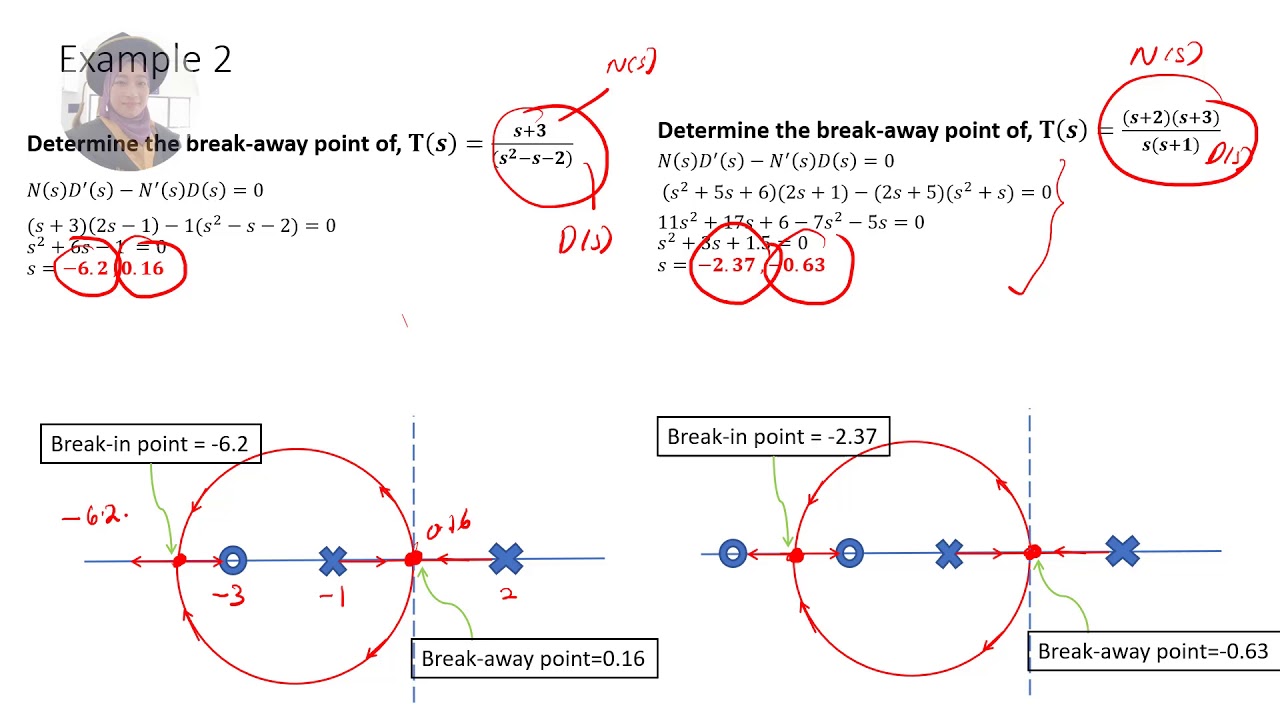
Photo Credit by: bing.com / locus root
Root Locus Plot Of Dynamic System - MATLAB Rlocus - MathWorks América

Photo Credit by: bing.com /
Control Systems How To Draw Root Locus - YouTube

Photo Credit by: bing.com / locus root draw
Sketching Root Locus Part 2 - YouTube
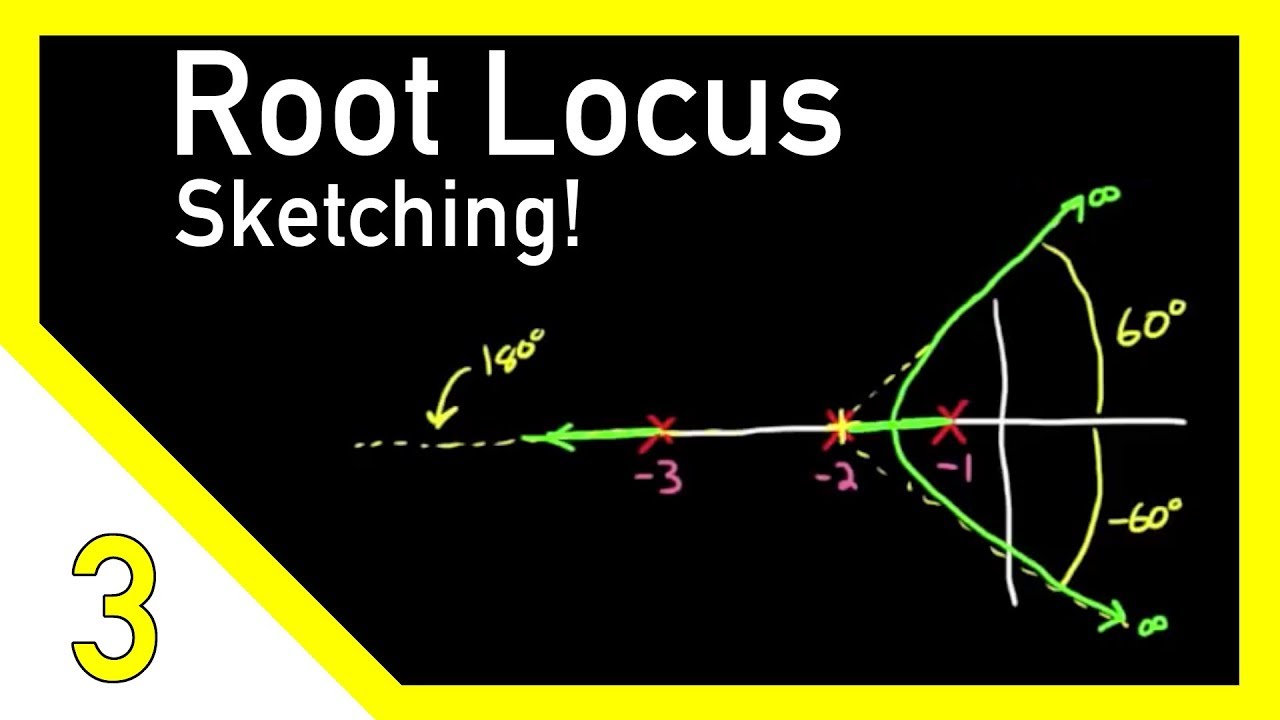
Photo Credit by: bing.com / locus root
How To Draw Root Locus | Solved Example
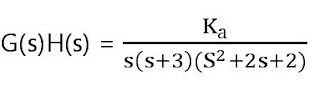
Photo Credit by: bing.com / root locus draw solved example varied





